BZR - 2.3.2 Ergebnisse

Inhalt --

2.3.1 zeitliche Oszillation: Versuchsaufbau -- 2.4 Versuche: räumliche Oszillation

2.3.2 Ergebnisse

Standardansatz

Abbildung 3 zeigt eine Reihe von Fotos eines Becherglases mit einem Standardansatz der BZR (siehe Tabelle 2). Man kann deutlich den Farbwechsel von rot nach blau beim Übergang von Ferroin nach Ferriin erkennen. Die Fotos entstanden in einem Abstand von etwa 5 s. Damit ergibt sich die Periodendauer der Reaktion zu ungefähr 30 s.

Abb.3: Fotos des Verlaufs der BZR mit Ferroin

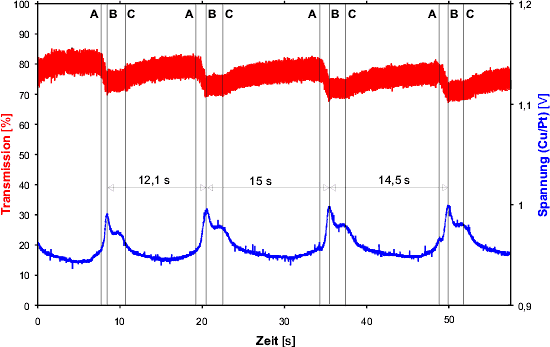
Abb.4:Messkurve des Standardansatzes. Transmissionskurve bei $\lambda$ = 626 nm (rot) und Spannungsdifferenz; Messintervall: 10ms; Temperatur: 23 °C ; Die Großbuchstaben kennzeichnen die gleichen wichtigen Punkte im Reaktionsverlauf, wie in Abbildung 1. [Datum: 1.12.2000]

Abbildung 4 zeigt Messkurven von vier Schwingungen eines Standardansatzes, bei dem die Menge des Ferroins von 1 ml auf 0,5 ml halbiert wurde. Die untere (blaue) Kurve stellt die Schwankungen der Spannungsdifferenz zwischen der Cu- und der Pt-Elektrode dar. Sie bezieht sich auf die rechte Achse. Die linke Achse gehört zur oberen (roten) Kurve und gibt die Transmission bei $\lambda$ = 626 nm an. Die gemittelte Periodendauer beträgt 13,9 s, was einer Frequenz von 0,072 Hz entspricht. Aus mehreren anderen Messreihen hat sich ergeben, dass die Abweichungen der Periodendauer vom jeweils errechneten Mittelwert bis zu 8 % beträgt. Die durchschnittliche Abweichung liegt zwischen 2 % und 3 % . ZHABOTINSKY gibt für die Frequenzstabilität über einige Perioden ,,1 % und höher`` [Zhabotinsky 1964] an.

Vergleicht man die Kurve der Spannungsdifferenz mit Kurven die für die Bromidkonzentration in der Literatur [Field u.a. 1972, Field, Schneider 1988, Kondepudi, Prigogine 1998] angegeben werden (siehe auch Abbildung 1), so erkennt man, dass sich diese weitgehend entsprechen. Die gemessene Spannungsdifferenz ist also ein Maß für die Bromidkonzentration. Es haben zwar auch die anderen Ionen einen Einfluss auf diesen Wert, er scheint aber für seine Änderung fast nicht von Bedeutung zu sein.

Schnelle Schwankungen der Lichtkurve (rot) um den Mittelwert machen diese zu einem breiten Band. Die Breite des Bandes beträgt je etwa 5 % des Mittelwertes nach oben bzw. nach unten. Diese Abweichungen entstehen durch die CO₂-Gasbläschen, die während der Reaktion im Gefäß aufsteigen und den Strudel, den das ,,Fischlein`` des Magnetrührers verursacht. Beide streuen das eingestrahlte Licht und ändern folglich die Intensität des ausgestrahlten Lichtes. Auf den bereits am Anfang beschriebenen Fotos der BZR (Abb. 3) kann man die eben erwähnten Gasbläschen gut sehen. Den Strudel kann man besonders in der blauen Phase als dunklen, keilförmigen Schatten am oberen Flüssigkeitsrand erkennen.

Die Transmissionskurve muss der Konzentration der roten Ferroin-Ionen proportional sein, da diese die Transmission im roten Spektralbereich der LED ,,steuern``.

Standardansatz mit Temperaturerhöhung

Es ist bekannt, dass sich die Reaktionsgeschwindigkeit vieler Reaktionen durch die Änderung der Umgebungstemperatur beeinflussen lässt. Dasselbe gilt auch für die BZR. Darum habe ich ein Experiment durchgeführt, in dem ich die Temperatur eines Standardansatzes kontinuierlich von etwa 23 °C (Zimmertemperatur) auf 44 °C erhöht habe. Die Aufheizung erfolgte durch die im Magnetrührer eingebaute Heizung. Zur Messung habe ich ein einfaches Quecksilber-Thermometer verwendet. Das Vorgehen beim Versuch blieb sonst unverändert. Abbildung 5 zeigt die Ergebnisse.

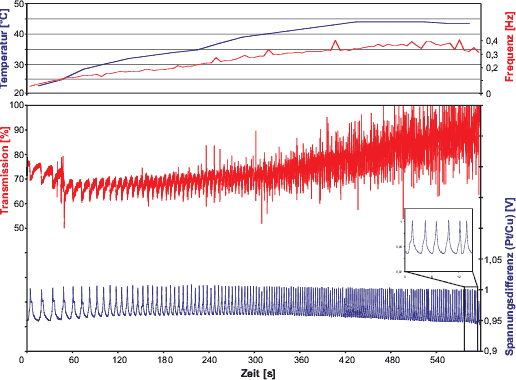
Abb. 5: Messung an der BZR mit Temperaturerhöhung. Oben: Temperatur (blaue Kurve) und Frequenz (rote Kurve). Unten: Transmission (rote Kurve) und Spannungsdifferenz (blaue Kurve); Messintervall: 10ms; Anfangstemperatur: 23°C ; Endtemperatur: 44°C ; für die Darstellung wurde jeweils über 6 Messwerte gemittelt [Datum: 1.12.2000]

Im oberen Diagramm zeigt die blaue Kurve den Anstieg der Temperatur und die rote die Frequenz der Schwingungen zum jeweiligen Zeitpunkt. Die Temperaturen wurden per Hand mitprotokolliert und in Abbildung 5 als Graph dargestellt. Die Werte für die Frequenzkurve wurden aus der Spannungskurve durch Ausmessen und Umrechnen bestimmt. Das untere Diagramm zeigt die Transmission bei $\lambda = 626$ nm und die Spannungsdifferenz zwischen Pt und Cu. Wie man sieht, nimmt die Frequenz der Schwingungen rapide zu, wenn man die Temperatur erhöht. Trägt man die Frequenz (als Maß für die RG) gegen die Temperatur auf, so erkennt man einen exponentiellen Zusammenhang, wie ihn die Arrhenius-Gleichung ( $k=A\cdot \mathrm{e}^{-E_a/RT}$ nach [Mortimer 1987]) beschreibt. Abbildung 6 zeigt diesen Graphen. In der Fortführung des beschriebenen Experiments konnte gezeigt werden, dass sich die ursprüngliche Periodendauer erneut einstellt, wenn man die Lösung wieder abkühlt. Die ,,Ausfransungen`` der Transmissionskurve werden umso stärker, je höher die Temperatur wird. Bei hohen Temperaturen kann man die eigentlichen Schwingungen gar nicht mehr ausmachen. Dies liegt daran, dass durch die Erhöhung der RG auch mehr CO₂ ensteht, das den Lichtstrahl, wie vorher beschrieben, beeinflusst.

Die Frequenzstabilität nimmt mit dem Anstieg der Temperatur ab. Dies sieht man am nicht mehr so glatten Verlauf der Frequenzkurve.

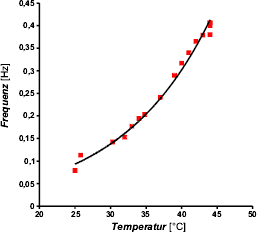
Abb. 6: Oszillationsfrequenz als Funktion der Temperatur der Lösung. Rote Punkte: gemessene Werte. Schwarze Kurve: angepasste Exponentialfunktion.

Standardansatz mit Erhöhung des pH-Wertes

Eine weitere Möglichkeit, die Oszillationsfrequenz der BZR zu variieren, ist die Erhöhung des pH-Wertes. Für diesen Versuch habe ich wieder einen Standardansatz verwendet, diesmal allerdings mit 1 ml Ferroin. Die Säure habe ich in 1 ml-Schüben (3 M H₂SO₄) aus einer Handpipette zugegeben.

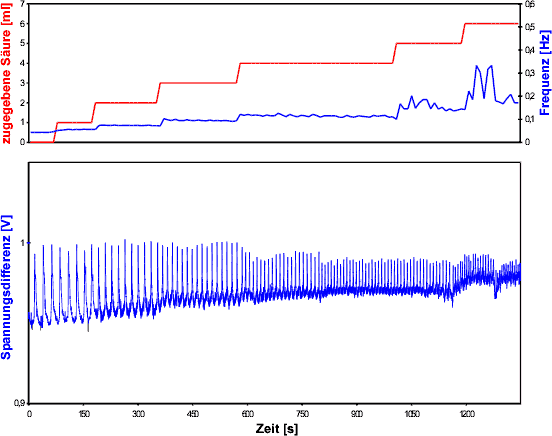
Abb. 7: Mesuung an der BZR mit schrittweiser Erhöhung des pH-Wertes. Oben: zugegebene Säuremenge mit c(H₂SO₄) = 3M (rote Kurve) und Frequenz (blaue Kurve). Unten: Spannungsdifferenz (blaue Kurve); Messintervall: 50ms; Anfangstemperatur: 24°C ; [Datum: 1.12.2000]

Abbildung 7 zeigt die Ergebnisse des Versuches. Die rote Kurve im oberen Diagramm stellt die Zugabe der Säure dar. Die blaue Kurve ist wieder die Frequenzkurve. Das untere Diagramm zeigt nur die Spannungsdifferenz, da die Transmissionskurve durch die Zugabe von Flüssigkeit sehr gestört und somit fast unbrauchbar ist. Zuerst fällt auf, dass sich die Spannungsdifferenz verkleinert. Sie ist am Schluss nicht einmal mehr halb so groß, wie am Anfang. Dies rührt wohl daher, dass sich die zugegebenen H₃O⁺-Ionen ebenfalls auf die Spannungsdifferenz auswirken, und somit der Effekt, den die restlichen Ionen auf diesen Wert haben, geringer wird. Dies wird dadurch untermauert, dass die Amplitude in Sprüngen abnimmt, die der Zugabe der Säure entsprechen. Des weiteren kann man sehen, dass sich die Frequenz der Oszillationen ebenfalls in Sprüngen mit der pH-Wert-Zunahme erhöht. Dabei fällt auch auf, dass hohe Säure-Konzentrationen die Stabilität der Oszillationen beeinflussen. Dies sieht man daran, dass die Frequenz umso stärker schwankt, je mehr Säure zugegeben wurde.Die Periodendauer betrug am Anfang - also ohne zugegebene Säure - ca. 23,3 s ( 0,043 Hz). Sie fiel bis auf etwa 5,5 s ( 0,182 Hz). Dies stellt fast eine Verfünffachung der Frequenz dar.

Standardansatz mit veränderter Ferroin-Konzentration

Dieser Absatz soll nur eine kurze Ergänzung zu den vorangegangenen Beschreibungen sein. Man kann nämlich aus den vorherigen Ausführungen noch eine weitere Möglichkeit zur Änderung der Oszillationsfrequenz herauslesen. Diese ist die Änderung der Ferroin-Konzentration, denn es dauert ja schließlich länger, mehr Ferroin zu oxidieren/reduzieren.

Im letzten Versuch (pH-Erhöhung) wurde doppelt soviel Ferroin (1 ml) verwandt, wie in den vorrausgegangenen (0,5 ml). Stellt man nun die Anfangsperiodendauern gegenüber, so stellt man fest, dass diese bei doppelter Ferroin-Konzentration auch fast doppelt so hoch sind. In den ersten beiden Versuchen hatte die erste Schwingung eine Länge von 13,9 s bzw. 12,6 s. Im letzten Versuch hingegen dauerte die erste Schwingung 23,3 s.

Standardansatz mit Mn²⁺/ Mn³⁺ als Katalysator

Die nun folgenden letzten beiden Versuche befassen sich mit der Variation des Elektronenüberträgersystems. Zuerst habe ich statt der Ferroin-Lösung eine etwa gleichkonzentrierte (0,001 M) Mn²⁺-Lösung verwendet. Diese erhält man aus 2 mg MnSO₄ * H₂O auf 10 ml Wasser. Von dieser Lösung habe ich etwa 1 ml eingesetzt.

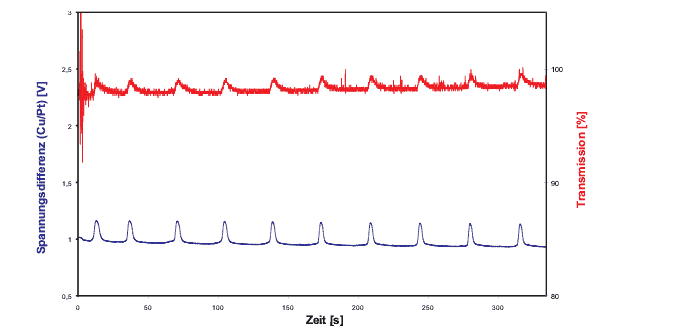
Abb. 8: Standardansatz der BZR mit 1 ml 0,001 M- Mn²⁺-Lösung als Elektronenüberträgersystem. Rote Kurve: Transmission. Blaue Kurve: Spannungsdifferenz (Cu/Pt). Messintervall: 50 ms [Datum: 1.12.2000]

Abbildung 8 zeigt die Ergebnise des Versuches. Die Transmission (blaue Kurve) ändert sich kaum sichtbar um 2-3%. Dafür ist die Amplitude der Spannungskurve (rot) mit 0,2 V etwa vier mal so hoch, wie bei Ferroin ( $\approx$ 0,05 V). Die Störungen am Anfang der Lichtkurve gehen darauf zurück, dass erst dort die Mn²⁺-Lösung zugegeben wurde. Darum wird bei der Berechnung der Periodendauern die erste Periode als Einschwingperiode nicht mitgewertet. Die durchschnittliche Periodendauer beträgt 34,8 s ( $\hat{=}$ 0,029 Hz) bei einer durchschnittlichen Abweichung von $\pm$ 0,7 s ( $\hat{=}$ 2,0 %). Damit ist die Periodendauer etwa 1,5-mal so groß, wie bei einem Ansatz mit Ferroin der gleichen Konzetration.

Da die Transmissionskurve hier horizontal spiegelverkehrt zur Transmissionskurve bei Ferroin verläuft, ist wohl die oxidierte DForm des Elektronenüberträgersystem (also Mn³⁺) farbbestimmend.

Standardansatz mit Ce³⁺/ Ce⁴⁺ als Katalysator

Dieser Versucht gleicht demjenigen mit Mn²⁺-Lösung. Nur wird hier statt dem System Mn²⁺/ Mn³⁺ das System Ce³⁺/ Ce⁴⁺ verwendet. Außerdem wurden 2 ml Ce³⁺-Lösung zugegeben, da bei Zugabe von 1 ml die Oszillation nach 2 Perioden aufhörte. Die 0,001 M Ce³⁺-Lösung erhält man, wenn man 0,055g Ammonium-Cer(IV)-Nitrat ( (NH₄)₂Ce(NO₃)₆) in 10 ml Wasser löst.

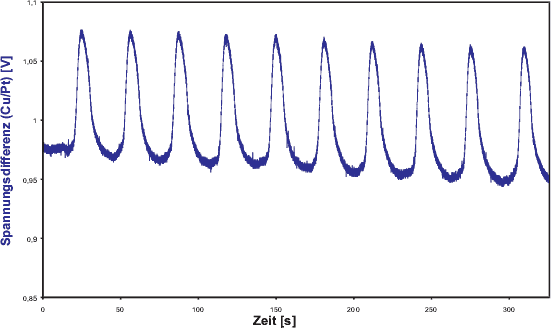
Abb. 9: Standardansatz der BZR mit 2 ml 0,001 M Ce³⁺-Lösung als Elektronenüberträgersystem. Blaue Kurve: Spannungsdifferenz (Cu/Pt). Messintervall: 50ms [Datum: 1.12.2000]

Abbildung 9 zeigt nur die Spannungskurve. Das Cer verursachte in der eingesetzten geringen Konzentration keine messbare Transmissionsschwankung. Die durchschnittliche Periodendauer liegt bei 31,7 s ( $\hat{=}$ 0,032 Hz) mit einer durchschnittlichen Abweichung von $\pm$ 0,9 s ( $\hat{=}$ 2,8 %). Durch die Zugabe von 2 ml Ce³⁺-Lösung können diese Werte wegen mangelnder Standardisierung nicht mit denen des Ferroins oder des Mangans verglichen werden.

Der ursprüngliche Ansatz von BELOUSOV

Abbildung 10 zeigt ein Becherglas mit dem Ansatz für die BZR den BELOUSOV in seinem ersten Artikel angibt. Leider ist der Farbunterschied nur schwer auszumachen. Deshalb wurden die Bilder digital etwas nachbearbeitet. Das Zeitintervall zwischen zwei Bildern beträgt etwa 5 s.

Abb. 10: Ursprünglicher Ansatz von B. P. BELOUSOV . Der Abstand zwischen den Aufnahmen beträgt 5 s.

BELOUSOV gibt folgendes Rezept an: ,,Nach unserer Erfahrung eignet sich für die Beobachtung der Verfärbung bei Zimmertemperatur besonders gut eine wäßrige Lösung, von der 10,0 ml neben Wasser 2,00 g Zitronensäure, 0,16 g Cersulfat, 0,20 g Kaliumbromat und 2,0 ml verdünnte Schwefelsäure (1:3) enthalten`` [Belousov 1959, Übersetzt von E. Gey, Berlin]. Die Oszillationsperiode beträgt hier etwa 25 s.