BZR - 3.3.2 Die Theorie zellulärer Automaten

Inhalt --

3.3 Simulation der räumlichen Reaktion -- 4 Zusammenfassung und Ausblicke

3.3.2 Die Theorie zellulärer Automaten

Zur Lösung des eben angegebenen DGS wird wieder ein iteratives Verfahren verwendet. Allerdings spielt sich die Simulation in einem zellulären Automaten (ZA) ab. Ein ZA ist ein Automat, der als Eingangszustand ein Feld von Zellen (1,2,3,...n-dimensional) in unterschiedlichen Zuständen hat und ein ebensolches ausgibt. Jede Zelle entspricht dabei einem Raumpunkt. Man kann sich z.B. ein solches zweidimensionales Feld wie ein Schachbrett vorstellen. Jedes Quadrat dieses Schachbrettes (eine Zelle) enthält die dortigen Konzentrationen der beteiligten Stoffe und wird über seine zwei Koordinaten angesprochen. Der Automat ändert nun diese Konzentrationen, indem er das Reaktions-Diffusions-System auf jedes Feld anwendet. Pro Zeiteinheit ändern sich also die Konzentrationen jeder Zelle genau einmal (durch Diffusion und Reaktion). Wurden alle Zellen bearbeitet, so wird das nun erzeugte neue Feld wieder als Eingangsfeld dem Automaten zugeführt (Iteration). Als Startfeld (t=0) wird eine zufällige Konzentrationsverteilung auf dem Feld eingesetzt [Weimar 1997]. Abbildung 19 verdeutlicht dieses noch einmal.

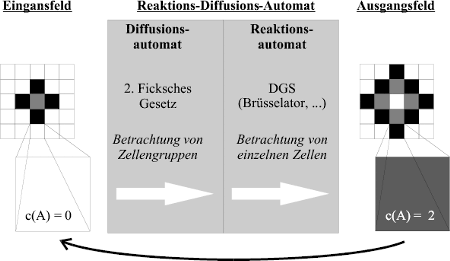
Abb. 19: Zellulärer Automat für ein Reaktions-Diffusions-System

3.3.3 Anwendung auf den Brüsselator

Das Modell, das ich auf einen zellulären Automaten übertragen habe, ist der Brüsselator. Dies erfolgte nach dem Prinzip, das ich in den letzten beiden Abschnitten beschrieben habe. Ich habe den Brüsselator zuerst für einen eindimensionalen Raum (Linie) implementiert. Das Programm dazu sieht wie folgt aus:

1 A <-- A₀
2 B <-- B₀

3 wiederhole für r = 0 bis r = Länge
4 X_t[r] <-- X₀ + Zufallsabweichung
5 Y_t[r] <-- Y₀ + Zufallsabweichung
6 Ende wiederhole

7 wiederhole
8 wiederhole für r = 1 bis r = Länge-1

9 $X_{t+1}[r] \leftarrow X_t[r] + D_x\cdot \left\{(X_t[r-1]-X_t[r])+(X_t[r+1]-X_t[r])\right\}\cdot \Delta t$

10 $Y_{t+1}[r] \leftarrow Y_t[r] + D_y\cdot \left\{(Y_t[r-1]-Y_t[r])+(Y_t[r+1]-Y_t[r])\right\}\cdot \Delta t$

11 Ende wiederhole

12   wiederhole für r = 1 bis r = Länge-1
13     n_X <-- k₁A + k₂·X_t[r]²·Y_t[r] - k₃·B·X_t[r] - k₄·X_t[r]
14     n_Y <-- k₃·B·X_t[r] - k₂·X_t[r]²·Y_t[r]
15     X_t₊₁[r] <-- X_t[r] + n_x·t
16     Y_t₊₁[r] <-- Y_t[r] + n_y·t
17   Ende wiederhole

18 Zeichne X_t[r] undY_t[r] für alle r als Linie
19 Ende wiederhole

Hierbei bedeutet X_t[r] (bzw. Y_t[r]) die Stoffmenge von X (bzw. Y) am Raumpunkt r zur Zeit t. In den Zeilen 1-6 des Programmes werden die Zellen des Raumes (Feldes) mit den Ausgangswerten X₀ und Y₀ plus einer zufälligen Abweichung (pos./neg.) gesetzt. A und B bleiben wieder an allen Raumpunkten gleich, um ein Fließgleichgewicht zu erreichen. Danach beginnt die Hauptschleife (Z. 7-19). In ihr wird zuerst die Diffusionsformel auf die X- und Y-Stoffmenge jeder Zelle der Linie angewendet (Z. 8-11). Danach werden die Reaktionsformeln für den Brüsselator (siehe 3.2.1) auf jede Zelle (jeden Raumpunkt) angewendet (Z. 12-17). Die bei der Diffusion auf X_t₊₁ und Y_t₊₁ zugewiesenen Werte werden jetzt als X_t und Y_t angesprochen. Das bedeutet, dass zu den Werten des Eingangsfeldes zuerst die Diffusion addiert wird und dann die Konzentrationsänderung durch die Reaktion, also

$\begin{displaymath}X_{t+1}[r]=X_t[r]+D_X\frac{\Delta ^2X[r]}{\Delta r^2}+f(X[r], Y[r]); \qquad \ldots\end{displaymath}$

Die so erhaltenen Ausgangsfelder mit den Stoffmengen X_t₊₁[r] und Y_t₊₁[r] werden nach der Ausgabe auf dem Bildschirm (Z. 18) wieder als Eingansfelder eingesetzt (Iteration). Interessant ist die Betrachtung der Randbedingungen des ZA. Diese beschreiben das Verhalten der Randzellen der Linie, da diese ja auf einer Seite eine nicht existente, also auch in Bezug auf X[r] und Y[r] undefinierte ,,Zelle`` haben, die aber in die Formeln eingeht. Im Falle meiner Implementierung verhalten sich diese Randzellen so, als hätten sie immer die Startkonzentrationen X₀ und Y₀.

Das eben beschriebene Programm habe ich wieder in Delphi umgesetzt. Abbildung 20 zeigt das ausgegebene Ergebnis. Entlang der Zeit-Achse (nach unten) werden einfach die Zustände der Zellen aufgetragen (Raumachse nach rechts).

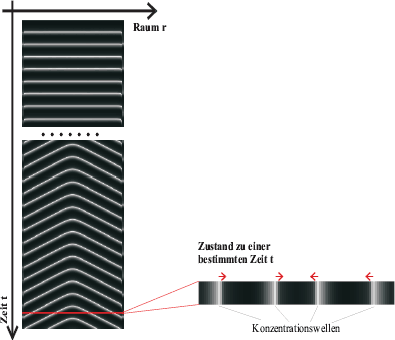
Abb. 20: Der Brüsselator als Reaktions-Diffusions-System auf einem eindimensionalen Raum (Linie). Parameter: k₁= k₂= k₃= k₄= 1; X₀= 1; Y₀= 1; A₀= 1; B₀= 3; t = 0,1; D_X= 0,1; D_Y= 0,01; Abweichung $= \pm 1$ 1 %; Länge = 100 Pixel; Farben: schwarz $\hat{=}\ X[r]=0$ X[r]=0; weiß $\hat{=}\ X[r]=0$ X[r]=5; eine Reihe zeigt den Stand nach jeweils 4 Rechenschritten

Wie man sieht, bilden sich ineinander verschachtelte Dreiecke. Dieses Bild bedeutet, dass Konzentrationswellen vom Rand aus (Störstelle) nach innen laufen und sich dort auslöschen. Dies ist ein Ergebnis, das schon ZHABOTINSKY im Experiment beschrieben hat. Er führte die BZR in einer dünnen Kanüle durch [Zaikin, Zhabotinsky 1970].

Nun habe ich den Brüsselator auf einen zweidimensionalen Raum (Fläche) übertragen. Daraus folgt, dass nun jeder Raumpunkt r zwei Koordinaten hat, nämlich r_x und r_y. Damit ist r formal der Vektor $\vec{r}={r_x \choose r_y}$ . Somit stelle ich die Konzentration von X an der Stelle $\vec{r}$ zur Zeit t als X_t[r_x, r_y] dar. Da ein Punkt auf einer Fläche mehr als nur zwei Nachbarn (wie bei der Linie) hat, muss man die Diffusionsformel entsprechend erweitern. Auf die Reaktionsformel hat die Änderung der Dimension keinen Einfluss, da sie sich ja nur auf eine Zelle bezieht. Wie ich bereits anfangs geschrieben habe, wird die Diffusion in meinem Programm implementiert, indem man den Mittelwert der Konzentrationsänderungen zu den Nachbarzellen, zur Konzentration der betrachteten Zelle addiert. Bei der Fläche stellt sich nun die Frage, welche Zellen man als Nachbarn ansieht. Für die Fläche gibt es hier hauptsächlich zwei verschiedene Möglichkeiten [Weimar 1997]:

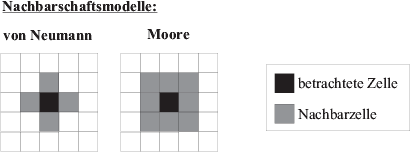
Ich verwende die einfachere von-Neumann-Nachbarschaft. Daraus ergibt sich folgende Formel für die Konzentrationsänderung $\frac{\Delta c}{\Delta t}$ durch die Diffusion:

$\begin{displaymath}\frac{\Delta c}{\Delta t}=D\cdot\left(\frac{c_t[r_x+1, r_y]+c...... r_y]+c_t[r_x, r_y+1]+c_t[r_x, r_y-1]}{4}-c_t[r_x, r_y]\right)\end{displaymath}$

(RD.3)

Um ein Programm zu schreiben, das obige Anforderungen erfüllt, kann man das Gerüst des Brüsselators auf der Linie verwenden. Man muss nur zwei Dinge ändern: 1. Die Diffusionsformel für die Linie muss durch Formel (RD.3) ersetzt werden. 2. Die Schleifen, die bisher die Linie anhand von r durchlaufen haben, müssen jetzt die Fläche anhand von $\vec{r}$ durchlaufen. Es muss also je eine zweite verschachtelte Schleife eingefügt werden, damit r_x und r_y durchlaufen werden. Dieses abgeänderte Programm sieht wie folgt aus:

1 A <-- A₀
2 B <-- B₀
3 wiederhole für r_x=0 bisr_x=Breite
4    wiederhole für r_y=0 bisr_y=Länge
5      X_t[r_x, r_y] <-- X₀ + Zufallsabweichung
6      Y_t[r_x, r_y] <-- Y₀ + Zufallsabweichung
7    Ende wiederhole
8 Ende wiederhole

9 wiederhole
10   wiederhole für r_x=1 bis r_x=Breite-1
11     wiederhole für r_y=1 bisr_y=Länge-1
12        $X_{t+1}[r_x, r_y] \leftarrow X_t[r_x, r_y] + D_x\cdot\left(\frac{c_t[r_x+1, r_y]+c_t[r_x-1, r_y]+\ldots}{4}-c_t[r_x, r_y]\right) \cdot \Delta t$
13        $Y_{t+1}[r_x, r_y] \leftarrow Y_t[r_x, r_y] + D_y\cdot\left(\frac{c_t[r_x+1, r_y]+c_t[r_x-1, r_y]+\ldots}{4}-c_t[r_x, r_y]\right) \cdot \Delta t$
14     Ende wiederhole
15   Ende wiederhole
16   wiederhole für r_x=1 bisr_x=Breite-1
17     wiederhole für r_y=1 bisr_y=Länge-1
18       n_X<--k₁·A + k₂·X_t[r_x, r_y]²·Y_t[r_x, r_y] - k₃·B·X_t[r_x, r_y] - k₄·X_t[r_x, r_y]
19       n_Y<-- k₃·B·X_t[r_x, r_y] - k₂·X_t[r_x, r_y]²·Y_t[r_x, r_y]
20       X_t₊₁[r_x, r_y] <-- X_t[r_x, r_y] + n_x·t
21       Y_t₊₁[r_x, r_y] <-- Y_t[r_x, r_y] + n_y·t
22     Ende wiederhole
23   Ende wiederhole

24 Zeichne X_t[r_x, r_y] und Y_t[r_x, r_y] für alle als Fläche
25 Ende wiederhole

Diesmal sind die Randbedingungen so gewählt, dass den Randzellen auf die gleiche Weise, wie den normalen Zellen zufällig schwankende X- und Y-Konzentrationen zugewiesen werden, die aber während der gesamten Simulation wie A und B konstant bleiben. Die Umsetzung des obigen Programmes in Delphi ergibt die Ausgabe in Abbildung 21. Unter den Bildern sind jeweils die verstrichenen Rechenschritte (Generationen) angegeben.

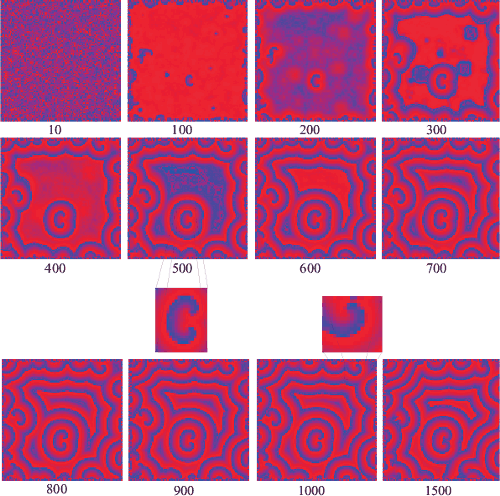
Abb. 21: Der Brüsselator als Reaktions-Diffusions-System im zweidimensionalen ZA. Aufgetragen ist die Konzentration von X. Zwei Spiralstrukturen sind jeweils vergrößert dargestellt. Parameter: k₁= k₂= k₃= k₄= 1; X₀= 1; Y₀= 1; A₀= 1; B₀= 3; $\Delta t=0,2;$ t = 0,2; D_x=0,2; D_y=0,02; Abweichung $= \pm 1000$ 1000 %; Breite = 100 Pixel; Farben: blau X[] = 0; rot X[] = 5.

Auf dem ersten Bild (10. Generation) sieht man den zufälligen Ausgangszustand des ZA. Auf den folgenden Bildern entstehen dann stabile Spiralenmuster. Der Rand wirkt aufgrund der Randbedingungen ebenfalls als Störzentrum. Von ihm gehen konzentrische Kreiswellen aus. Treffen zwei Wellenfronten aufeinander, so löschen sie sich gegenseitig aus. Die Farbgebung wurde in Anlehnung an das Experiment mit Ferroin/Ferriin gewählt.

3.3.4 Vergleich zwischen Simulation und Experiment

Die vom Brüsselator erzeugten Wellen (sowohl im ein-, als auch im zweidimensionalen Raum) gleichen in ihren Eigenschaften den chemischen Wellen, die ich im Experiment beobachtet habe (siehe Abbildungen 11 bis 13). Beide bilden konzentrische Kreise, die von Störzentren ausgehen und sich gegenseitig auslöschen, aber nicht von Hindernissen reflektiert werden. Die Simulation bildet auch Spiralwellen aus, die ich leider im Experiment nicht erzeugen konnte, über die aber in der Literatur berichtet wird [Kauffman 1996]. Abbildung 22 zeigt solche Spiralmuster in der BZR.

Abb. 22: Gegenüberstellung der Spiralmuster in der BZR (Quelle: [Kauffman 1996, Seite 87]) und der Simulationsergebnisse.

Der Brüsselator ist also auch in ein- und zweidimensionalen Systemen dazu geeignettrotz seiner Einfachheit die komplexen Phänomene der BZR nachzubilden. Die Umsetzung meines eigenen und des FKN-Modell schlug fehl. Beide zeigten keine sich ausbreitenden Wellenstrukturen. Somit sind sie wohl eher dazu geeignet gerührte Systeme zu simulieren.

Inhalt --

3.3 Simulation der räumlichen Reaktion -- 4 Zusammenfassung und Ausblicke

druckbare Version