BZR - 3.2.3 Ein eigenes Modell

Inhalt --

3.2.2 FKN-Modell -- 3.2.4 Vergleich

3.2.3 Ein eigenes Modell

Der folgende Teil beschreibt ein Modell, das ich selber entwickelt habe. Es simuliert einen etwas anderen Aspekt der BZR. Die beiden ersten Modelle (Brüsselator und FKN) bilden thermodynamisch offene Fließgleichgewichtssysteme nach. Im Idealversuch wird die BZR auch so durchgeführt. Wegen des großen apparativen Aufwands, der zur Herstellung eines Fließgleichgewichtes erforderlich wäre (Durchflussreaktor ...) habe ich sie allerdings in einem geschlossenen System (Becherglas) angesetzt. Indem man die Konzentrationen der Edukte im Vergleich zu der des Katalysators Ce³⁺ sehr hoch ansetzt, kommt man hier einem Fließgleichgewicht sehr nahe. Dabei werden durch die geringe Konzentration des Katalysators immer nur sehr kleine Stoffportionen umgesetzt. Nun war die Frage interessant, ob man auch ein Modell entwickeln könnte, das ein solches geschlossenes System simuliert. Meine ersten Versuche, bei denen ich die schon vorgestellten Modelle einfach um Gleichungen für die Änderung der Edukt- und Produktkonzentrationen erweitert habe, hatten keinen Erfolg. Die Systeme näherten sich immer ohne Oszillation dem Gleichgewichtszustand an.

Ich habe dann einen ganz anderen Ansatz zur Simulation verwendet. Wie im ersten Teil der Arbeit beschrieben, kann man die BZR so erklären, dass mehrere Reaktionen gleichzeitig ablaufen (Reaktionsgleichungen I-II). Von diesen wird Reaktion (II) durch Bromid-Ionen inhibiert, die in Reaktion (I) abgebaut und in Reaktion (III) rückgebildet werden. Dieses Konzept habe ich nun in ein Simulationsmodell umgewandelt. Nur die Produktion von HCOOH und CO₂ wird nicht mitsimuliert. Ich habe um den oben beschriebenen Mechanismus für die BZR einen sog. Automaten aufgebaut. Ein Automat ist ein theroretisches Gebilde der Informatik. Er ist eine Art Black-Box, die eine Reihe von Eingangszuständen in eine Reihe von Ausgangszuständen wandelt. Dabei besitzt ein Automat einen inneren Zustand, der angibt, wie die Eingangszustände zu verarbeiten sind. Am Ende jeder Verarbeitung geht dann der Automat in einen neuen inneren Zustand über, oder bleibt im aktuellen [Mittelbach 1997].

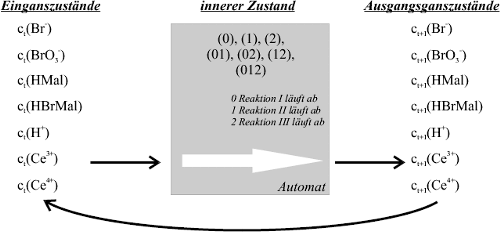
Der Automat, den ich verwende hat die Stoffmengen zur Zeit t als Eingangszustände und gibt die neuen Stoffmengen zur Zeit t+1 aus. Sein innerer Zustand gibt jeweils an, ob Reaktion (I), (II) oder (III) gerade abläuft. Es sind auch Kombinationen der Reaktionen möglich. Der Automat ersetzt also im in 3.2.1 beschriebenen Grundprogramm das DGS. Seinen Aufbau zeigt Abbildung 16.

Abb. 16: Schematische Darstellung des verwendeten Automaten

Die Bedingungen für das Ablaufen der einzelnen Reaktionen sind:

$\bullet$ Reaktion (I) läuft immer ab, wenn die Ausgangssubstanzen in genügender Konzentration vorliegen:

$\begin{displaymath}n(\mathrm{Br^-})>0;\qquad n(\mathrm{HMal})>0;\qquad n(\mathrm{BrO_3^-})>0;\qquad n(\mathrm{H^+})>0;\end{displaymath}$

$\bullet$ Reaktion (II) läuft immer ab, wenn die Ausgangssubstanzen in genügender Konzentration vorliegen und (fast) kein Bromid vorhanden ist:

$\begin{displaymath}n(\mathrm{BrO_3^-})>0;\qquad n(\mathrm{HMal})>0;\qquad n(\mathrm{Ce^{3+}})>0;\end{displaymath}$

$\bullet$ Reaktion (III) läuft immer ab, wenn die Ausgangssubstanzen in genügender Konzentration vorliegen:

$\begin{displaymath}n(\mathrm{HBrMal})>0;\qquad n(\mathrm{Ce^{4+}})>0;\end{displaymath}$

Reaktion (II) wird durch Bromidionen inhibiert. Sie läuft nur ab, wenn keine Bromid-Ionen vorhanden sind, darum gilt die Bedingung $n(\mathrm{Br^-})\rightarrow 0$ . Um festzustellen, ob eine Konzentration gegen null geht, wird sie mit einer vorher festgelegten Grenze verglichen. Liegt sie darunter, so wertet der Automat diese Konzentration als gegen null gehend. Der Grenzwert wird in Prozent der Ausgangskonzentration angegeben (Grenzstoffmenge). Es ist übrigens egal, ob man von Konzentrationen, oder Stoffmengen spricht, weil das betrachtete Volumen gleich bleibt.

Für die drei möglichen Reaktionen erhält man folgende Ablaufgeschwindigkeiten:

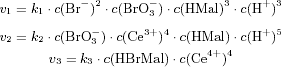
Daraus ergeben sich folgende Konzentrationsänderungen (DGS):

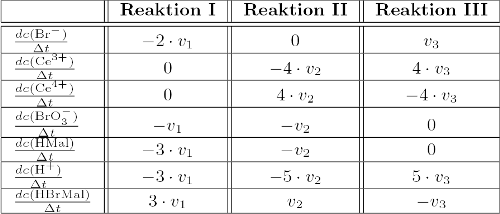
Das Simulationsprogramm (Listing folgt weiter unten), das im Grunde demjenigen für den Brüsselator entspricht wird in der Haupt-Schleife (Z. 2-19) also folgendes tun: Zuerst werden die Geschwindigkeiten v₁ .. v₃ für die Reaktionen (I) ... (III) ausgerechnet (Z. 3-5) Danach wird überprüft, ob Reaktion (I) ablaufen könnte (Z. 6). Falls ja, dann läuft sie ab (Z. 7-9). Danach wird dasselbe Spiel für Reaktion (II) (Z.10-13) und (III) (Z.14-17) durchgeführt. Zum Schluss werden die Änderungen auf dem Bildschirm ausgegeben (Z. 18):

1 setzen der Simulationsvariablen auf Startwerte
2 wiederhole
3 $v_1 \leftarrow k_1 \cdot c_t(\mathrm{Br^-})^2 \cdot\ldots$
4 $v_2 \leftarrow k_2 \cdot c_t(\mathrm{BrO_3^-}) \cdot\ldots$
5 $v_3 \leftarrow k_3 \cdot c_t(\mathrm{HBrMal}) \cdot c_t(\mathrm{Ce^{4+}})^4$
6    wenn Reaktion I ablaufen kann, dann
7 $c_{t+1}(\mathrm{Br^-})\leftarrow c_{t}(\mathrm{Br^-}) + \frac{\Delta c(\mathrm{Br^-})}{\Delta t}$
8      ...
9    Ende wenn
10   wenn Reaktion II ablaufen kann, dann
11 $c_{t+1}(\mathrm{BrO_3^+})\leftarrow c_{t}(\mathrm{BrO_3^+}) + \frac{\Delta c(\mathrm{BrO_3^+})}{\Delta t}$
12     ...
13   Ende wenn
14   wenn Reaktion III ablaufen kann, dann
15 $c_{t+1}(\mathrm{Br^-})\leftarrow c_{t}(\mathrm{Br^-}) + \frac{\Delta c(\mathrm{Br^-})}{\Delta t}$
16     ...
17   Ende wenn
18   Zeichne Graphen der berechneten Stoffmengen
19 Ende wiederhole

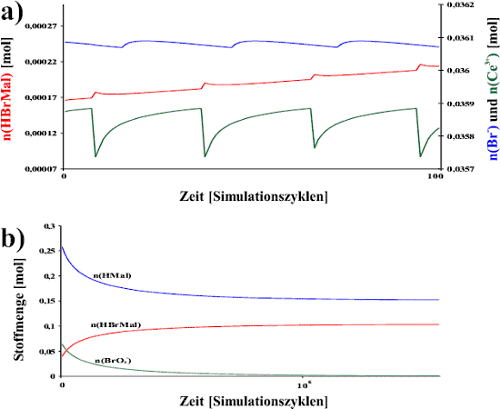
Abb. 17: Funktionsgraphen meines eigenen Modells. Startwerte (entsprechen den Bedingungen der Experimente aus 2.3): k₁ = 5*10³; k₂ = 2*10¹²; k₃ = 8*10¹¹; t = 1; n(Br^-)= 0,024 mol; n(BrO₃^-)= 0,08 mol; n(Ce³⁺)= 0,0002 mol; n(Ce⁴⁺)= 0; n(HMal)= 0,3 mol; n(HBrMal)= 0; n(H⁺)= 1 mol; Grenzkonzentration: 1% * c₀ ; a) Rechenschritte/Punkt = 1; b) Rechenschritte/Punkt = 10000;

Auch dieses Programm habe ich in Delphi umgesetzt. Es gibt die Kurven in Abbildung 17 als Ergebnis aus. Graph a) zeigt den Verlauf von drei Oszillationsperioden. Es sind die Stoffmengen von Bromid (blau), Brommalonsäure (rot) und Ce³⁺ (grün) gegen die Anzahl der Reaktionszyklen ( $\hat{=}$ Zeit) aufgetragen. Graph b) zeigt den Verlauf einer Simulation bis zur Einstellung der Oszillation (1,5 * 10⁶ Zyklen). Hier sind die Stoffmengen der Edukte Bromat (grün) und Malonsäure (blau) und des Produktes Brommalonsäure (rot) gegen die Zeit aufgetragen. Die Geschwindigkeitskonstanten k₁ .. k₄ habe ich experimentell bestimmt, indem ich von den ungefähren Verhältnissen der Geschwindigkeiten ausgegangen bin die sich aus dem Mechanismus der BZR ergeben (siehe Abschnitt 2.2).

Ein Vergleich mit dem Experiment erfolgt im nächsten Abschnitt. Hier soll aber auf einige Erkenntnisse über das beschriebene Modell hingewiesen werden, die sich aus den Graphen ergeben: Zum einen sieht man vor allem an Diagramm a), dass die Produktion der Brommalonsäure (jeweils die rote Kurve) in kleinsten Schüben vor sich geht. Insgesamt nähert sich die Konzentration der Brommalonsäure immer langsamer einem bestimmten Grenzwert an, der von der Ausgangskonzetration an Malonsäure und der Menge der gebildeten organischen Produkte (HCOOH und CO₂) abhängt. Der kleine Einbruch bei der Brommalonsäure rührt daher, dass diese in Reaktion (III) wieder verbraucht wird. Die Oszillation kommt zum erliegen, weil sich die Bromat-Konzentration gegen null bewegt. Das gesamte System enthält vier oszillierende Variablen. Diese sind die gezeigte Bromid- (blau) und Ce³⁺-Konzentration (grün). Dazu kommt die der Ce³⁺-Konzentration spiegelverlehrt verlaufende Ce⁴⁺-Konzentration. Außerdem oszilliert der pH-Wert, weil in Reaktion (I) und (II) H⁺-Ionen aufgebraucht und in (III) wieder gebildet werden. Betrachtet man aber die Bilanz, so nimmt der pH-Wert leicht ab, weil mehr H⁺-Ionen verbraucht, als gebildet werden (siehe Summengleichung (IV)).

Inhalt --

3.2.2 FKN-Modell -- 3.2.4 Vergleich

druckbare Version